Calculating the Odds of Every Laff-a-Lympics Event

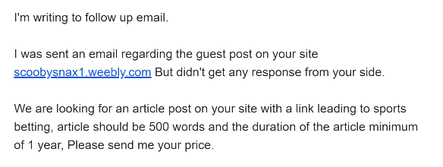
About 3 months ago on May 12, I received perhaps one of the strangest emails I've ever gotten, telling me that I did not follow through with my promise to write a 500 word post about "sports betting" on my blog. Granted, no such promise was actually made on my part, and it was just some random scammer trying to fool me. I did find the email quite amusing though, as it made no sense why the person would think I would post an article related to sports betting on a Scooby-Doo blog.

I was talking with one of my best friends, Bradford N. Smith, about this humorous email I received and the ridiculousness of the person thinking they could somehow trick me into thinking I had forgotten to fulfill my end of the bargain posting an article completely unrelated to Scooby. After joking about it for a little while, we had an amazing idea: what if we actually made this happen as a joke by tying it to Scooby in some way? We quickly realized that Laff-a-Lympics would provide the perfect opportunity for writing an article about "sports betting."

For this article, just in time for the end of the 2020 Tokyo Olympics, we calculated what the odds would be of all 103 Laff-a-Lympics events through taking into account each individual player's previous results for each event they participated in. In simpler terms, using Scooby as an example, if Scooby had placed third two times and second one time in his three previous events he had participated in, and Yogi had placed second one time and first two times in his three previous events, then the odds would predict it was more likely for Yogi to win, because he had a better history of winning. Taking into account each player's performance in all previous events they had been in, each player's average placing against their opponents, and a combination of the team's average placing, we took the average of what place they came in for every single event to determine how likely it was that they would win.

Once the averages were all taken, I converted the averages into odds. We started off the odds at 3:1, given there are three teams. 3:1 means that the player has not played any previous events and is equally likely to come in any place. If it was likely given the player's average that the team would place first, the odds went down to 2:1. If it was likely the player would place second, the odds went up to 4:1. If it was likely the player would place third, the odds went up to 6:1. Note that we rounded up for the averages, so if the average was 1.83, we rounded it up to the next whole number, which in this case would be 2. However, rounding up occasionally caused a problem if two players' averages were very close. For example, if Blue Falcon's average was 1.75 and Doggie Daddy's average was 1.84, they'd both round up to 2 under our rule, even though Blue Falcon would be slightly more likely to win given the lower average. In the cases where this occurred, I adjusted the odds to reflect this by making the odds 3.5:1 if the player was slightly more likely to come in first, and 5:1 if the player was slightly more likely to come in second. There were some cases where the odds were tied. It was equally likely for two teams to place first. I will return to this later when we get into the "betting" part of this sports betting article.

For ease of understanding, since this is a more statistics/number-driven article than I've ever posted here before, let's say you start off with $10. In each match, you bet $1 that your team will come in first. You always place your bet on whatever team has the most likely odds of winning. If two teams are equally likely to win, we will say that you choose not to bet. If your team wins, you win a dollar. If the team you bet on loses, you lose one of your dollars.

If you bet on 73 events (30 of these events had two or more teams equally likely to win, so you wouldn't bet), you would end up owing $1. You would also lose the $10 you started with.  In 42 cases, you would lose a dollar, but you would win a dollar in 31 cases, which balances out where you would only owe $1.

In this scenario, the odds would tell you to bet on the Yogis 26 times. 17 of those times you lost, and you won 9 of the times. The odds pointed towards the Scoobies winning 42 times. You won 25 of these times, while losing 17 of these times. Lastly, you only bet on the Rottens 3 times, and you lost every single time you bet on them.

Let's take this in a different direction, because perhaps you'd always want to bet on the same team. If you always bet on the same team without taking odds into account, starting with $10 and getting a $1 for every win (and losing a $1 for every time your team lost), how much would you end up with?

Let's say I bet on the Scooby Doobies every time, not even taking the odds into account. I would win 51 out of 103 times, and lose 52 of those times. I would wind up losing one of the dollars you started with, and would walk away with 9 out of your original 10 dollars. If B bet on the Yogi Yahooeys every time, he would win 38 out of 103 times, meaning he would lose 65 times. He would not only lose his original $10, but he would end up owing $27. If someone were bet on the Rottens every time, which you really shouldn't do lol, you'd win 30 times while losing 73. You would lose your original $10 and owe $43.

Compiling this data did also brought out some really interesting statistics. Dastardly Dalton was the only Really Rottens player with an average that's as good as some of the players on the Yogi Yahooeys and the Scooby Doobies. Snooper and Blabber from the Yogis came out with the best average of any players, with a shocking 1.0. Blabber never loses anytime he competes, though he only competes in three matches, which is the least amount of events participated in by any player (tied with Mr. Jinks). also Mrs. Creepley and Junior Creepley from the Rottens were both tied for the worst average, 2.67. Junior Creepley never wins any match he's a part of. Brenda Chance holds the worst average for the Scoobies, which is 2.13. For the Yogis, Huckleberry Hound has the worst average, at 2.0. Daisy Mayhem, Yogi Bear, Captain Caveman, and Grape Ape competed in the most events out of all the players, each tied for a shocking 19.

More specifically, there are some additional interesting statistics regarding players' opponents. Mr. Jinks is the only character that never competed against another player more than once. On a similar note, Hong Kong Phooey and Dixie are the only players to compete against only one player more than once. On the opposite end of the spectrum, Blue Falcon competes against Doggie Daddy 7 different times, and Captain Caveman competes against Grape Ape 7 times, tying for the most times the same two players competed against each other. The record for the most players played against more than once is 20, and is held by both Captain Caveman and Quick Draw McGraw.

To conclude this article, we'd like to share all the data we gathered for this article and give an overview of our research, which you can download below. The first tab of the Excel spreadsheet, Betting Odds, has an overview of all the players competing in each event, and the odds that they will win. In the last column, I specified whether relying on the odds would cause you to win your bet, lose your bet, or walk away with the same amount of money you started with (even). This is the final data we used for this article that shows the odds for each event, determining whether you'd win or lose. In the second tab, Match Breakdown, a breakdown of how each game played out is provided, showing the participants of each match, and what place the team came in. In the third tab, Individual Breakdown, a breakdown is provided by character of what place they're coming in for each match they participated in, followed by overall average, total disqualifications and ties, and average by appearance which shows how their average changed over time as they competed in more events. In the final tab, Challenger Breakdown, a detailed breakdown of what place a character came in (the left column) against specific opponents (the top row) is given.

This data took a long time to pull together because there were so many variables involved.  I want to give a huge thank you to B for putting hours upon hours of time into compiling and calculating this data so we could publish this article together. I spent about five hours taking the averages of the data, coming up with the odds and doing some general cleanup, but that's honestly nothing compared to how much B did. He compiled every bit of the data about each individual character and he should get most of the credit for the amazing spreadsheet we created. I'm so lucky to have such a dedicated, generous person in my life!

I hope you all enjoyed our presentation of the data, and I've provided the Excel file of all of our data below, which you can download.

laffalympics.xlsx
File Size:	54 kb
File Type:	xlsx

Download File

---